Portrait of a real model

This is by far the drawing that I am most satisfied with. He's a friend of my teacher and he was very kind to come to the studio last Sunday and let us draw him.

This drawing didn't take me very long but when I was done I just couldn't take my eyes off it. I know it's not perfect but I, for the first time, feel a hint of the presence of the person that I drew. 

Yes I know, presence is a very abstract word. But this is how the drawing of a photo and a real person is different. If properly done, you feel life, you feel the personality, you feel the warmth and texture. Time is frozen and the soul is kept.

Not that I am suggesting I did it. But at least I know where should I go, and it's all that matters :)

The epic fail of a numbers game....LOL

One of my great friends sent me this video the other day for me to appreciate the beauty of the divine symmetry of a circle. I am certainly grateful to his thoughtfulness, especially when I found it infinitely amusing to watch and I almost fell off my chair laughing...because...

* It was so outrageously wrong *

And the mistakes were so trivial that I have to write about it... haha..

Now watch it first..

For the sake of whoever reading this I am skipping all the mathematics. Let's not miss the fun part. But in case you want a full mathematical proof, tell me. This video claimed that the theory was from Nikola Tesla [Read Here]. But I really doubt it. If to my total ignorance, that any of the things I mentioned below is wrong, please let me know.

#1 God may have created the beauty of a circle but he did not make it 360 degrees. Human did. There is nothing divine about it and there is no code.

As to the first question why there are 360 degrees, you can take a historical approach [Read here]. I believe we keep using it because it is a handy number (i.e. it has a lot of factors). If say, we have 100 degrees in a circle instead, how many degrees are there in an internal angel of an equilateral triangle? 16.66666666666666... degrees (instead of the elegant 60). 

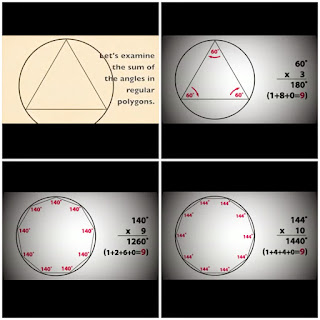
#2 When we bisect a circle and sum up the digits of an angle. It doesn't always 'reduce' to 9. 

First of all, why do we have to sum all the digits of an angle by the way. This is making no mathematical sense. But since it's the rule of the game, let's follow.

If a circle is a cake, we cut it once, each slice has 180 degrees. True.
We cut it twice, each slice has 90 degrees. Still True.
We cut it 3 times, each slice has 60 degrees. *FAIL*

His theory only works if we cut the cake in a power of 2 number of times. i.e. 2, 4, 8, 16....

#3 The sum of the internal angles of a polygon doesn't always 'reduce' to 9, too

Well...there is actually an easier way to do so. The sum of all interior angles of a polygon equals to:

(no. of sides - 2) X 180

So what about a polygon with 13 sides? 1980. *FAIL*
(Of course if you sum 1 and 8 it gives 9 too. But there is nothing magical about it. It's just a characteristic of all multiples of 9....)

#4 No. We don't call this a "singularity"...

If we divide 1 by 0, this is a singularity. It appears when a mathematical function is indifferentiable or discontinuous. [Read here]

#5 Nor a "vacuum", unless he's referring to quantum mechanics... 

*shake head* [Read here]

#6 These are not vectors "communicate" an "outward divergence", unless he's referring to fluid mechanics...

*sigh* [Read here]  

#7 This is not linear duality either. It's a programming technique for optimization...

*cross arms*  [Read here] 

#8 Yes this is meaningless. But no this is not even numerology. This is just a (failed) numbers game.

*face palm* [Read here]

# 9 And above all, his explanation of all these "reduce to 9" thingy left me speechless....

"9 models everything and nothing simultaneously"... I wonder if I should understand this sentence as science or literature, because neither way seems to make any sense....

My infinite astonishment converges elegantly into a single exclamation of

W.T.H.